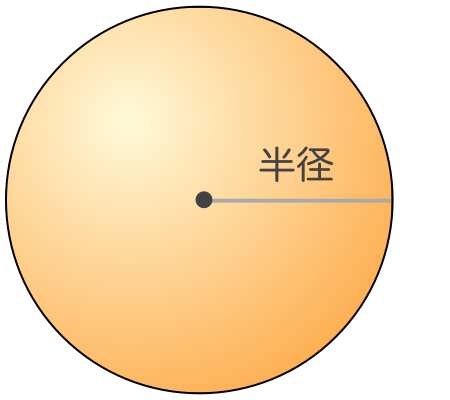
2 球 どこから見ても円に見える形を球といいます。球の切り口も円の形になっています。 球を半分に切った時、その切り口の様子は右上の円の図と同じようになっています。 ただし、円の「中心」「半径」「直径」と区別するために、「球 では冒頭の考え方を使って、内接球の半径を求めてみましょう。 内接球の中心を点 I I 、半径を r r とすると、 半径rの球の体積を求める公式は、次のようになります。 πは円周率 (=)です。 球の体積は、半径rの3乗に比例していくということですね!
球の体積 簡単に計算できる電卓サイト
球の半径の求め方 小学生
球の半径の求め方 小学生-球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に 球が内接しています。この球の半径を求めなさい。 解説 平面における、「三角形と内接円の関係」とほぼ同じです。 空間図形においても、着目すべき「平面」で解きます。



大学入試問題
ここで上記の第3式において、 A, B を距離を求めたい2点、 C として北極 N = ( π / 2, 0) を取る。 図は以下の通り ( 山口大学のサイト より引用)。 この時、以下の事実が成り立つ。 角 c は円弧 A, B を通る大円の角となり、これが求める中心角 x である。 角 C球の慣性モーメントを2通りの方法で導出します。 その半径 は, R 2 − z 2 \sqrt{R 求め方も教えていただけますでしょうか。 3 順像法と逆像法の違いについて教えてください 4 ムーアヘッドの不等式を利用して3変数の相加・相乗平均不等式を示したい電卓の使い方 体積を求める球の半径を入力して「計算」ボタンを押してください。 体積は割り切れない場合に分数で回答することもあるため、分数でも表示しています。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπと
(ポイント)半径rの球の表面積の公式 半径rの球の表面積をSとすると S=4πr2 (例2)次の球の表面積 を求めなさい。 (解答) 上の図より、球の半径は 6cmなので、 半径rの球の表面積の公 式のrに6を代入すると、 2=144π r=6を代入 答 144πcm2 球の表面積を 3辺が与えられた三角形の外接円の半径rは、 正弦定理 で求めます。 6辺が与えられた四面体の内接球の半径rは、 四面体abcd=( abc abd acd bcd)r/3 で求めます。 では、6辺が与えられた四面体の外接球の半径rは、どうやって求めるのでしょうか。となります 三角形の面積は,いろんな求め方がありますそこで, ヘロンの公式など を用いて三角形の面積を求めておくと,内接円の半径が求まります ヘロンの公式 三辺の長さが a , b , c である三角形の面積 S を求めるには まず、 s= abc2nnnnn を
はがし方① 下図のように切り込みを入れてはがす。 横の長さ=球の一周分の長さ= 2πr 縦の長さ=球の半周分の長さ= πr 形を単純にしてだいたいの面積を求める. 面積= πr × 2πr × 1 2 = π2r2 = 314πr2 形を切り落として考えているため,実際の面積は一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波解き方を確認! 問題(ニューアクションβより) 半径1㎝の球があり、今後この球の半径は毎秒1㎝の割合で大きくなっていく。 球の表面積Sおよび体積Vの5秒後の変化率を求めよ。 まずは、SとVの式を作りましょう。 そして、それらを微分することで



Sphere 01



球体の半径の求め方 球の周を40kmとして 球の半径は約何km Yahoo 知恵袋
r(a b c) の3次元バージョンです。 内接球の半径,表面積,体積のうち2つ分かれば残りの1つも分かる という公式ですが,ほとんどの場合表面積と体積から内接球の半径を求めることに球の表面積の求め方 公式と計算例 Scipursuit 表面積の求め方 球 球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r



球の問題 苦手な数学を簡単に




内接球の半径を求める一般的な公式 高校数学の美しい物語
高校数学Ⅰ三角比四面体の体積と内接球の半径求め方まとめと問題 四面体の体積と内接球の半径を、三角比を用いて求める解き方について解説しています。 正四面体の体積、内接球の半径の公式も「たしかめ」用に紹介してます。 1 四面体の体積と 逆に 円周の長さ 2πr を 半径 r で積分すると 円の面積 πr^2 になる。 球の体積 4/3πr^3 を 半径 r で微分すると 球の表面積 4πr^2 、逆に 球の表面積 4πr^2 を 半径 r で積分すると球の体積** 4/3πr^3 となる。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円




立体の内接球 外接球に関する問題のチャートを作りました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




三角錐の内接球の半径の求め方を四角錐でも使うことが出来るのですか Clear
球の半径をrとすると、体積の求め方は、 4/3πr³ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。 外接球半径求め方, 球に関する問題(その2) 半径(内接球): ルート6/12球の中心はah上にある。 ④ abcにおいて,oは外心。 ①球の中心を通り,底面の 三角形と平行な面で切った 断面 abcにおいて,oは内心。 球はすべての面に接する。 頂点aから底面 bcdに下 ろした垂線の足をh,bcの 中点をmとする。 球はすべての面に接する。半径4cmの球の体積を求めてください! ※円周率はπ Clear 数学 中学生 5年以上前 あやξ*′ ′ )⚡ 半径4cmの球の体積を求めてください! ※円周率はπ
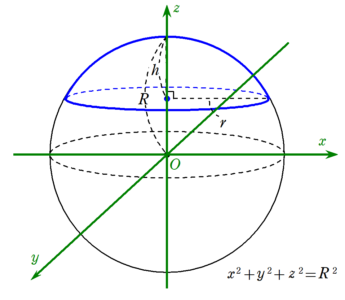



球欠と球冠 Fukusukeの数学めも




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ
接触球は、接触円と同様な考え方のもので、くぼみに(点や線でなく面で)接触する最大の球です。 接触球が半径rのところでの曲面の曲率Kは、 です。 単位半径の球面の曲率Kは1です。 ふつうの平面は、接触球の半径が無限大 になりますから、その曲率Kは0球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 円と球の空間 半径ではなく,直径で使えるようになること。 半径を直接測定したり取扱う機会はあまりない。 いちいち半径の公式から換算するのは能率が悪い。 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積 公式と計算問題と証明 Irohabook
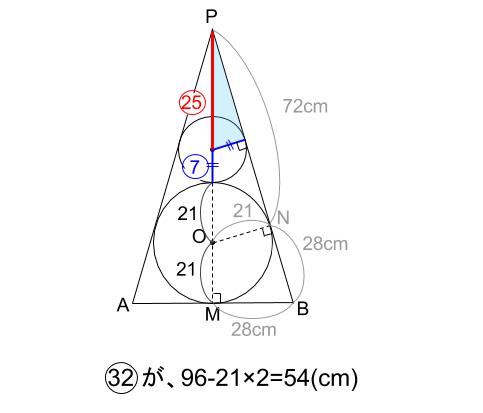
球と球も接しています。このとき、小さい球の半径を求めなさい。 解説円錐と内接球・その1の追加問題です。下の大きい球の半径は、問題1と完全に同じ求め方により、\(21cm\) と求まります。 ここまで求めた状態から、次に上の小さい球の半径を求めます。豚肉を今日もいためたね。 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、裁ったとき切りとられた球の部分の表面積と切りとられた円柱の部分の側面積の 等しいことまで証明している。答 正四角錐の内接球の半径 図のように、底面積が 4m 2 で1つの側面の面積が 5m 2 の正四角錐に球が内接しています。 この球の半径は? 解答1 面積の条件より、底面の1辺は 2m、側面の二等辺三角形の高さは 5m になります。




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
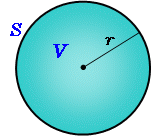



球の体積 高精度計算サイト




球の半径を求める 3つの方法 Wikihow
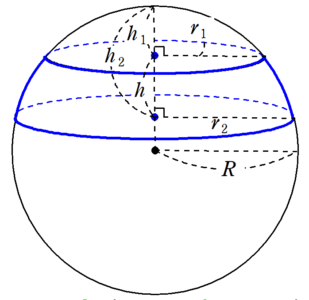



球台と球帯 Fukusukeの数学めも




解説 三角錐に内接する球の半径を求めよう 理系のひとりごと



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積 公式と計算問題と証明 Irohabook
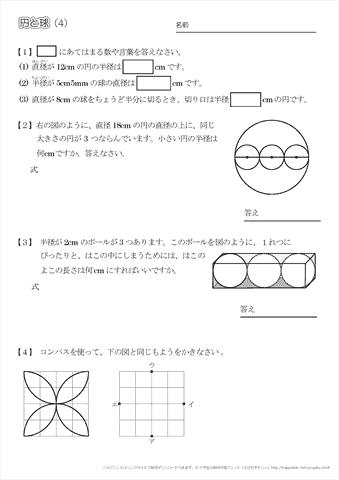



小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生
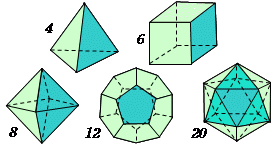



正多面体の体積 高精度計算サイト



円錐と内接球 その2 中学数学の無料オンライン学習サイトchu Su
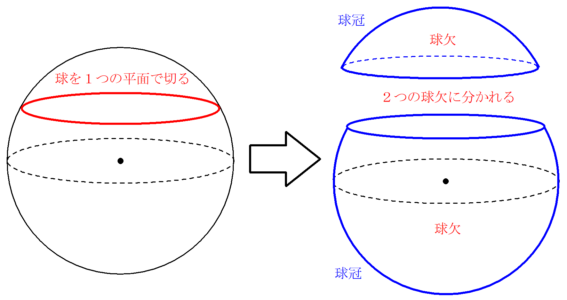



球欠と球冠 Fukusukeの数学めも




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




球の表面積の求め方 公式と計算例
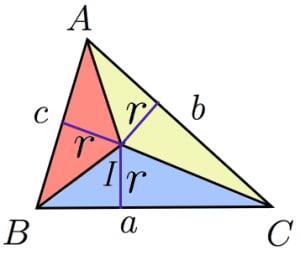



内接球の半径を求める一般的な公式 高校数学の美しい物語




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




高校数学 正四面体の計量 表面積 2面のなす角 高さ 体積 内接球の半径 外接球の半径と立方体への埋め込み 受験の月




球の表面積の求め方 その3 感じる科学 味わう数学
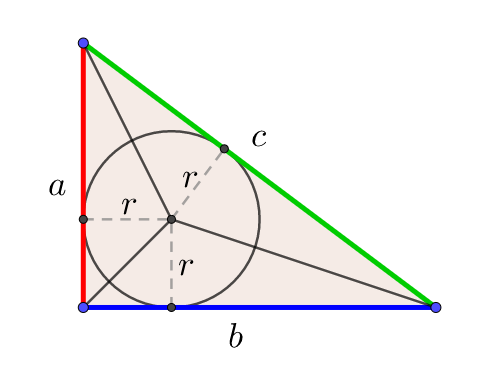



解説 三角錐に内接する球の半径を求めよう 理系のひとりごと



Www Pref Fukushima Lg Jp Uploaded Attachment Pdf




円周の求め方 公式と計算例




球の体積 簡単に計算できる電卓サイト




高校化学基礎まとめ 金属結晶の充填率の求め方 Mm参考書



球の表面積の公式の求め方



Q Tbn And9gctjav6gvj1k5jlr5jeyhgdtl 5v264jxhqxszqv9lgkyrvbr9tp Usqp Cau




球の半径を求める 3つの方法 Wikihow
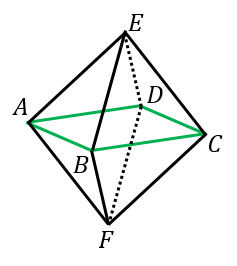



正八面体の体積 表面積 外接球の半径 内接球の半径 具体例で学ぶ数学



U9j580gf8iba369ji2w Xyz P 296




高校数学 三角比 四面体の体積と内接球の半径求め方まとめと問題



Math 立体に内接する球 働きアリ



教えてください ある球の半径を2cm長くすると表面積が80pc Yahoo 知恵袋




球の表面積と体積の公式 数学fun



正八面体の表面積 体積 半径



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
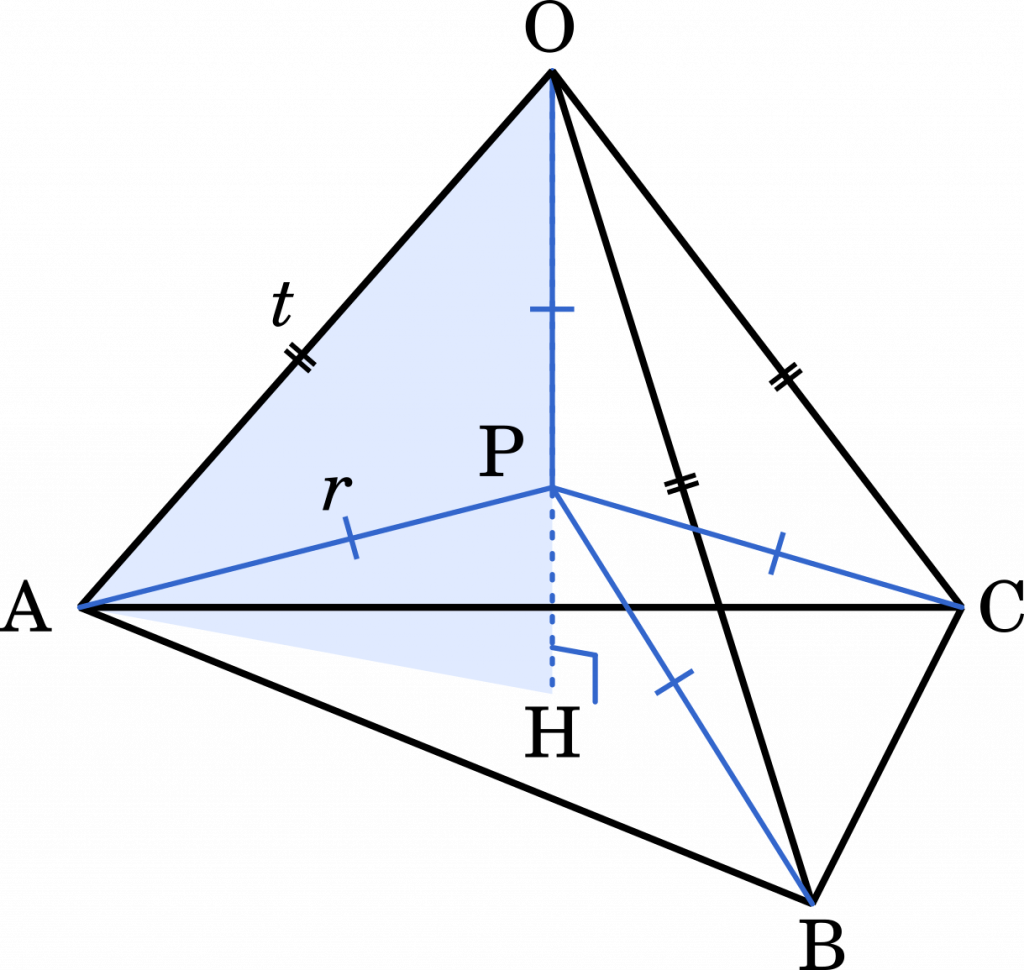



数ia 外接球の半径を考える 千葉大 Mm参考書



球の表面積の公式の求め方



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




空間図形 内接球と外接球 Youtube




高校数学 三角比 四面体の体積と内接球の半径求め




小学3年生の算数 円と球 練習問題プリント ちびむすドリル 小学生




高校数学b 球面の方程式 1 練習編 映像授業のtry It トライイット
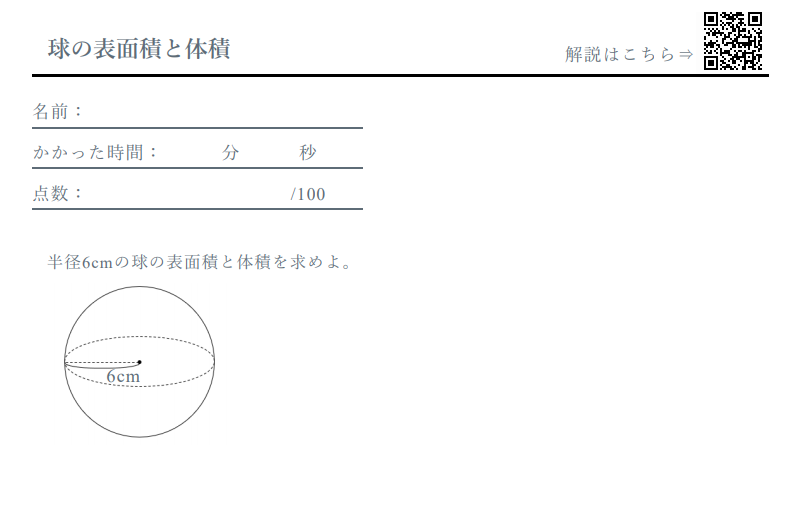



球の表面積と体積 計算ドリル 問題集 数学fun




中学 数学 テクニック 内接球の半径の求め方 高校入試 高校受験 裏ワザ Youtube




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
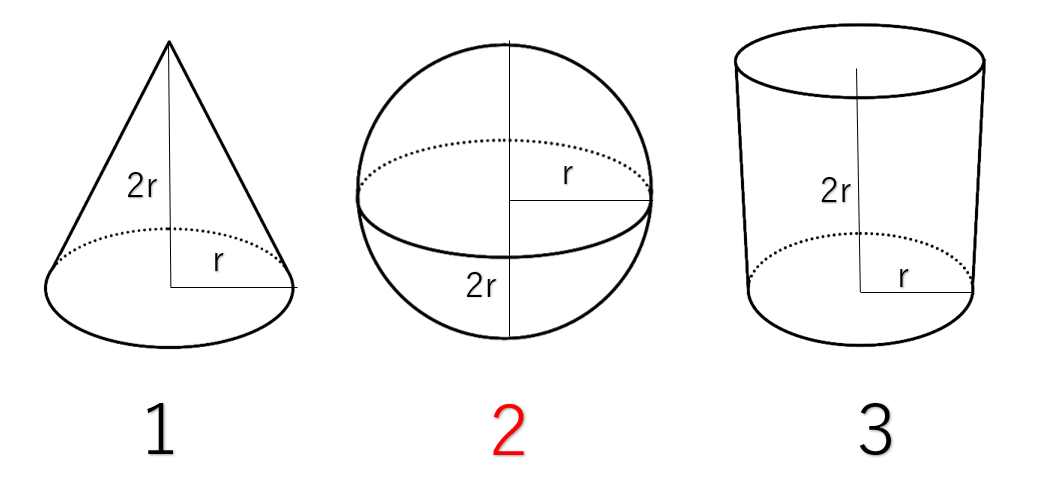



中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾



1



円錐の底面の半径が3 母線の長さが6です この球の半径の求め方 Yahoo 知恵袋
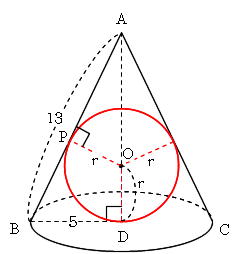



Mathematics 三平方の定理 5 空間図形と三平方の定理 働きアリ




球の表面積と体積の公式 数学fun



半径5cmの球の表面積と体積を求めよ 教えてください Yahoo 知恵袋




球の半径を求める 3つの方法 Wikihow



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




三角錐の内接球の半径の求め方を四角錐でも使うことが出来るのですか Clear




球体の表面積 積分で求める方法 うちーノート




球の表面積と体積の公式 数学fun




球の半径を求める 3つの方法 Wikihow



1




中1 数学 6 5 球の体積 表面積 Youtube




球面レンズの焦点距離の求め方 光と色と




この球体の体積の求め方を教えてください それと私は数学の公式をすぐに忘れてしまうので Clear




高校数学 正四面体 外接球の半径 オンライン無料塾 ターンナップ Youtube




球の表面積と体積の公式 数学fun




内接球 外接球の求め方についてです 2枚目の赤で書いているところが理解出来ません Clear




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen



球の中心の求め方 Inak Engineering Llc




球の半径を求める 3つの方法 Wikihow
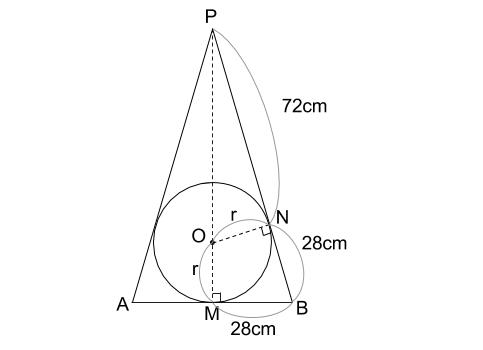



円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su




Python演算処理 半径 直径 円周長 円の面積 球の表面積 球の体積の計算上の往復 Qiita



大学入試問題



三角錐に内接する球の半径の求め方 こんにちは中学三年ですが Yahoo 知恵袋




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の表面積 体積 身勝手な主張




円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su



1



中1数学 球の表面積と体積の定期テスト過去問分析問題 Atstudier




半球の体積と表面積を計算する 具体例で学ぶ数学
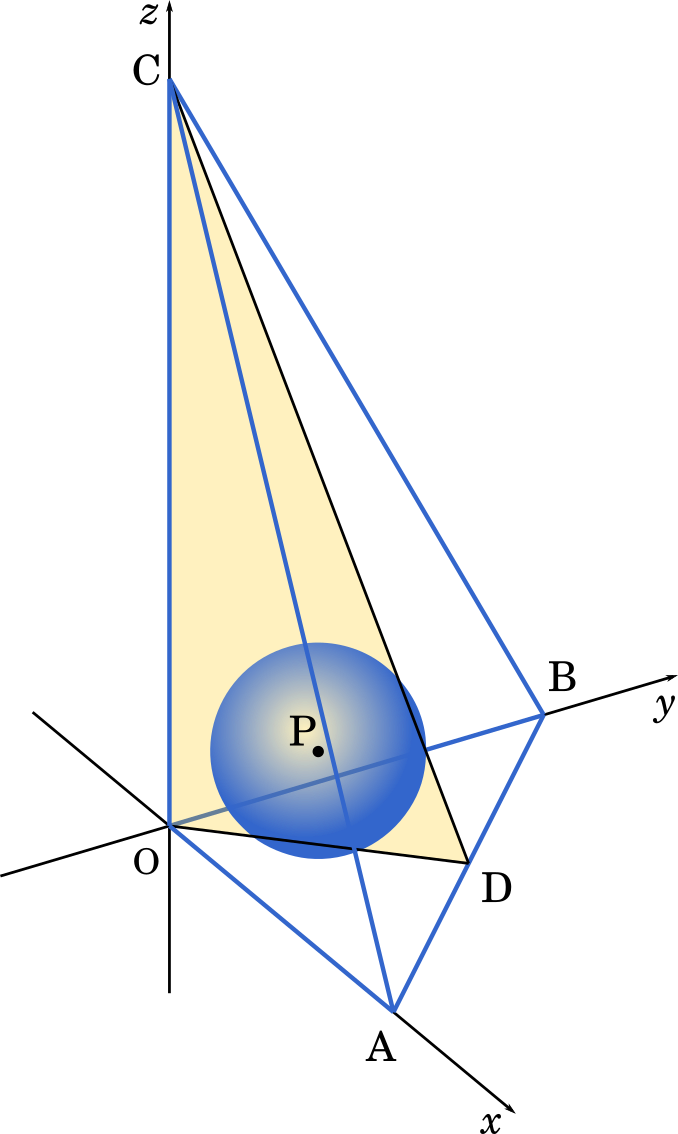



九州大21理系第1問 数iib点と直線の距離 正四面体でない四面体の内接球の半径を求める Mm参考書




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ




球面の方程式の求め方と問題の解き方をわかりやすく



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ




球体を切った時の直径の求め方 球体を切った時の直径の求め方を教えて 数学 教えて Goo




高校 三角錐に内接する球の半径 Ab Ac Ad 6 Cd Db 6 2で 数学 教えて Goo




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
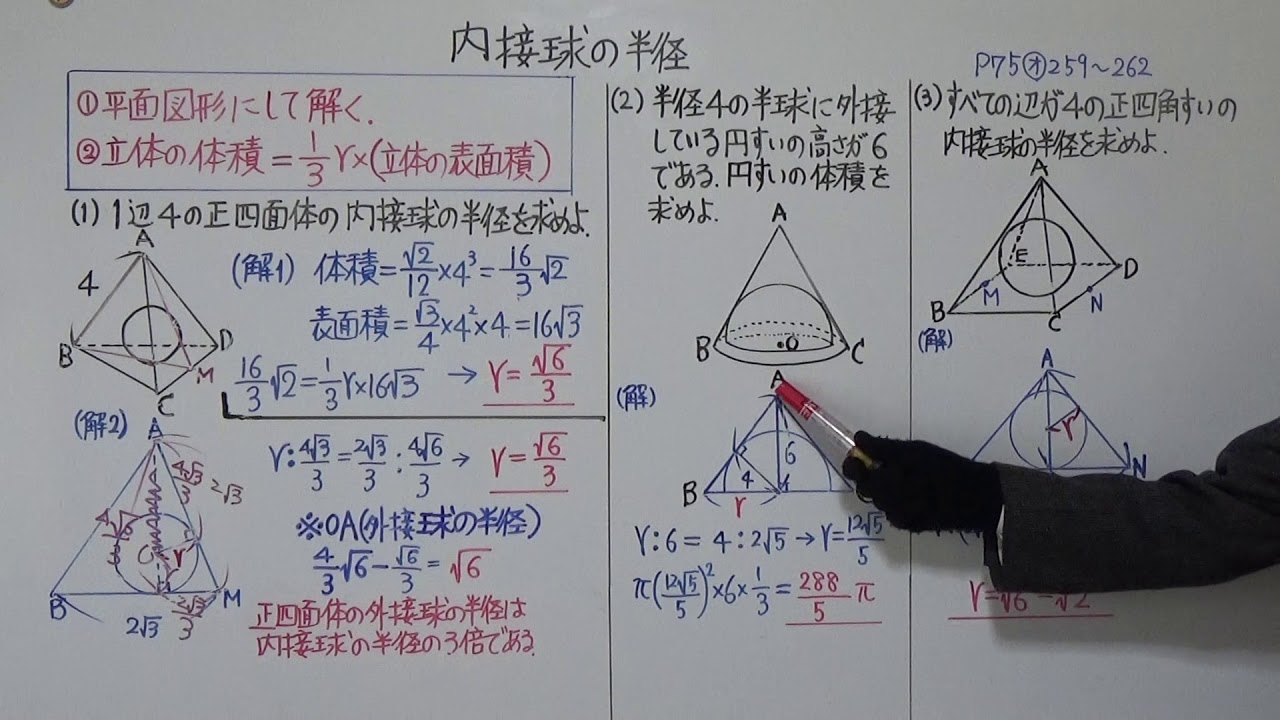



58 内接球の半径 Youtube



球の表面積と体積の求め方 苦手な数学を簡単に



0 件のコメント:
コメントを投稿