2
通过本课程的学习,要求研究生掌握分数阶微积分和分数阶微分方程的基本理论和方法,为学习后继课程、开展科学研究打好基础。 二、课程内容与学时分配 第一章 预备知识(4学时) 1.1 Gamma函数和 Beta函数 1.2 MittagLeffler函数 1.3 MittagLeffler函数的Laplace 考虑下面分数阶微分方程的初值问题, Caputo意义下的分数阶微分算 众所周知,上述初值问题可以等价于下面的积分方程, 该方程等价于差分方程这里, ,是离散步长。从 公式(4)可以看到 形式上依赖于 在整个区 献可以全部由来代表。
分数微分方程
分数微分方程- dy/dxは分数ではないが、、、 は、分母分子の を約分して、 とすることはできません。 で一つの記号であり、 を で割ったものでも、 分の を意味しているわけでもありません。 しかし、 は、計算上は分数として扱うことができます。 合成関数の微分を学習すると、そのことが理解でき参考文献薛定宇《分数阶微积分学与分数阶控制》 数值实现 Matlab 19a 主要基于薛定宇开发的FOTF工具箱蜜酒厅通讯社 固体地球物理学部前情回顾形式主义的居士:分数阶微积分和分数阶微分方程数值实验(7)——分

分數微分口訣3 Wfklee
2.1分数阶微积分运算的线性性与Leibnitz公式 本节我们针对Riemann—Liouville分数阶积分、微分的定义给出分数阶积分Dg口f(t)、 微分掰厂(f)的一些重要性质,这些性质在现实中经常用到,以此把整数阶积分 d一"dt一、微分矿Sldt"推广到分数阶。我研究过分数阶微分方程这方面,简单谈谈,一点陋见,欢迎批评指教。 我觉得不管是整数阶还是分数阶 微分方程最重要的两个问题就是 拟合 和 求解一是能不能构建出一个合适的方程来拟合我的实际问题,分数阶由于其可以很好地刻画遗传性和记忆性质等>logの微分例題を解説!分数、合成関数はどうやる? こちらの記事でまとめているのでご参考ください。 微分のやり方まとめ! お疲れ様でした! 数学Ⅱまでに学習する微分の計算は、とてもシンプルで簡単なものばかりでした。
この点も含めて『分数関数の微分のやり方(商の微分公式)を誰でもわかるように解説』で解説しています。 4 応用 ここでは大学レベル以上で学ぶことになる公式を列挙します。 41 逆三角関数の微分 逆三角関数の微分は次の通りです。 微分作用を立ててかくには,通常分数のコマンド \frac{}{} を用います。分数のかき方のテクニックは,LaTeX分数のかき方とテクニックも参照してください。 physicsパッケージの場合は,デフォルトではローマン体 \mathrm{d} で出力されます。の導関数(微分)を求めてください. (解答) 分子 x の微分は 1 ,分母 x 2 −1 の微分は 2x だから 例題1 の関数 を微分してください. 解説を読む ア) 商の微分法でやる場合 分子は (やられてから)− (やり返す) (分母)2 を使うと
分数微分方程のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 | ||
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
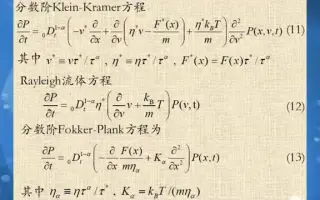 |  | |
 | 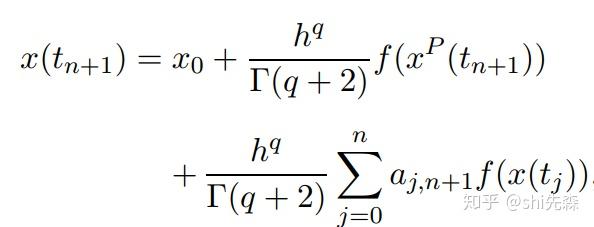 | |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
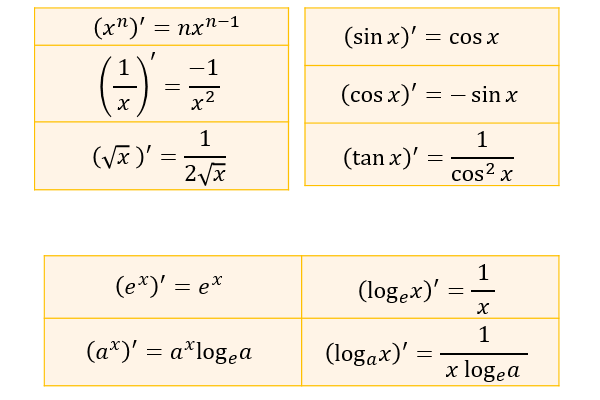 |  |  |
 |  | |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「分数微分方程」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
第一讲 分数阶微分方程 主要参考资料4,5,7 11 分数阶导数 分数阶导数(Fractionalderivatives)有多种定义方式,常用的有RiemannLiouville分数阶导数,Caputo分 数阶导数,GrünwaldLetnikov分数阶导数,等等 下面我们就对以上三种定义进行分别介绍,更多定义可参 见3 几类分数阶微分方程解的稳定性分析 Lyapunov稳定性理论在自动控制、动力系统、生物种群等自然科学和工程技术等方面有着广泛的应用 本文主要利用Lyapunov第一方法讨论分数阶微分方程在不同条 件下解的渐近稳定性及利用Lyapunov第二方法讨论微分方程解的Mittag
Incoming Term: 分数 微分, 分数微分公式, 分数微分方程,




0 件のコメント:
コメントを投稿